Yet Another Article on Zippers, in Erlang
What are zippers?
In Erlang (and in many other programming languages which include a functional subset), operations on purely functional data structures are frequently limited to O(log n) time complexity: there is no such thing as a true array with constant time access. No destructive updates. Nothing like pointers either.
Because of this, you end up with a bunch of modules like array, dict, gb_trees and whatnot, which are all built either on lists or trees with varying branching factors. None of them do better than O(log n), and list-based solutions don't do better than O(n) (although they can average n/2.)
There is, however, a class of data-structures that allow for amortized constant time for some operations: finger trees and zippers are examples of this.
So let's say you are writing a text editor and you need to hold a list of all the events typed in the currently open document. The naive implementation with standard data structures such as lists would force something a bit like [{TimeN, ChangeN}, {TimeN-1, ChangeN-1}, ..., {Time1, Change1}}]. That is, every time the user modifies the document, an entry of the form {Time, Change} is added to the beginning of the list.
What happens when the user wants to go back in history? A lot of programmers might just borrow the non-functional 'array and indexes' method: we keep a counter in memory (which acts like an index), and when the user presses some 'back' button, the index becomes N+1, N+2, etc. Conversely, when the user presses 'next', we remove 1 from that number:
1> lists:nth(1,[current,recent,old,older,oldest]).
current
2> lists:nth(2,[current,recent,old,older,oldest]).
recent
3> lists:nth(3,[current,recent,old,older,oldest]).
old
4> lists:nth(2,[current,recent,old,older,oldest]).
recent
This approach is directly based on how we're used to deal with arrays or dictionaries that support constant time access. Sadly, it's rather inefficient with functional data structures: the access time in the example above is O(n). If the document's history contains thousands of changes and the user loves to go through them, you end up doing a bunch of useless lookups, all the time. It's even worse if you allow the user to update the history and whatnot: not only do you need to traverse the list for lookups, but you need to rewrite a good part of the data structure every time you update it.
A valid alternative solution is to store everything we have traversed before in a secondary structure in order for the 'current' element to always be accessible in constant time. Instead of storing something like {3,[d,c,b,a]}, you'd store {[c,d],[b,a]}, or more generally: {Previous, [Current|Next]}, where Previous (the history of visited items) and Next (those left to go through) are both lists and Current is a single term. See the code below for an idea of how this works with more detail.
Not only does this approach make the current element accessible in constant time, but the previous and next one too! This lets you use the list a bit as a doubly-linked list in languages that support them, as in you can hold a 'pointer' to the current list location, and you can iterate backwards and forwards with little overhead. Moreover, changes to the list can be made in constant time (once you're at the right position) and the cost of modifying the elements is spent only when going backwards in the list.
Well that's a zipper. In this particular case, this would be a zipper with a list. Zipper is a generic term used to qualify a data structure that you can arbitrarily modify and navigate through.
I don't know if I'm being clear enough, but I nevertheless suggest the following articles if you want to get real information on zippers, rather than just my own little primer:
- Zipper (data structure) on Wikipedia
- Zippers with trees on Haskell wiki
- You could have invented zippers
- Theseus and the Zipper
I especially recommend the last link (the part before type differentiation). It's the one I found the easiest to understand, although you need to be able to grasp Haskell's type system to understand it.
Zipper lists
So as described above, a list that we can go through in both directions [because we store seen elements] is a zipper, and can be implemented by holding a list/stack of all the elements we went through. Here's an implementation of zipper lists (abbreviated to zlists) according to the {Previous, [Current | Next]} structure:
-module(zlists).
-export([list_to_zlist/1, zlist_to_list/1,
prev/1, next/1, current/1,
replace/2, insert/2, delete/1,
map/2, rmap/2]).
%% A zlist, or zipper list, allows to 'browse' a list
%% in two directions, much like a doubly-linked list.
%% Access to the next and previous element are both
%% constant time, and so is the cost of insertion and
%% deletion.
%% Lookups remain O(n).
%% {Previous, [Current | Next]}.
-type zlist() :: {list(), list()}.
%% Most zippers data structures wouldn't really need to convert between
%% types, but lists are kind of ubiquitous in usage, so it might be
%% proper to convert them.
%% Convert from standard list to zlist
-spec list_to_zlist(list()) -> zlist().
list_to_zlist(L) when is_list(L) -> {[], L}.
-spec zlist_to_list(zlist()) -> list().
zlist_to_list({Pre, Post}) -> lists:reverse(Pre) ++ Post.
%% Zipper lists can be moved inside in both direction, much like a
%% doubly-linked list in languages that support them. The functions
%% prev/1 and next/1 allow to move in such a manner. They crash whenever
%% you reach the end or the beginning of the zlist, exactly like the
%% functions erlang:hd/1 and erlang:tl/1 do.
-spec prev(zlist()) -> zlist().
prev({[H|T], Post}) -> {T, [H|Post]}.
-spec next(zlist()) -> zlist().
next({Pre, [H|T]}) -> {[H|Pre], T}.
%% current/1 allows to read the value of the list. fails on empty
%% zlists, exactly the way erlang:hd/1 does. Also fails on lists where
%% the end has been reached.
-spec current(zlist()) -> term().
current({_, [Current|_]}) -> Current.
%% Replace changes the value of the current zlist item.
-spec replace(term(), zlist()) -> zlist().
replace(Val, {Pre, [_|Post]}) -> {Pre, [Val|Post]}.
-spec insert(term(), zlist()) -> zlist().
insert(Val, {Pre, Post}) -> {Pre, [Val|Post]}.
-spec delete(zlist()) -> zlist().
delete({Pre, [_|Post]}) -> {Pre, Post}.
%% Map and reverse maps as an example of potentially
%% useful functions
map(_, L = {_, []}) -> L;
map(F, {P, [H|T]}) -> map(F, {[F(H)|P], T}).
rmap(_, L = {[], _}) -> L;
rmap(F, {[H|T], N}) -> rmap(F, {T, [F(H)|N]}).
Not every useful function is implemented here. As an example, it could be nice to have an extract(zlist()) -> {term(), zlist()} function that removes the current value from the list while returning it, but I consider such functions to be shortcuts around the functions already presented here.
The zlists module could be used to implement the history feature mentioned in the first section of this post. You'd only need to use the prev/1, next/1, current/1 and insert/2 functions to do it.
Here's the link to the zlists module if you want it, and the unit tests module that goes with it. The unit tests are in a separate file because the error assertions would piss dialyzer off for the type checks.
Zipper Binary Trees
Zipper lists are conceptually simple enough to be easy to reinvent and replace with queues. More interesting are trees, because storing the history of how you go through them is a bit more complex.
Let's imagine a 'Book where you are the hero.' A simplified version of such a book could be represented as a decision tree where you can pick 'yes/no' to a question. Picking 'yes' goes to the right node, and picking 'no' goes to the left one. Each of these nodes then have more questions until you die or succeed. Going down such a decision tree is trivial. What's more interesting is when you need to go back one or more levels up in the tree to change your mind because you died and feel like cheating.
You could use a queue or zipper list to store all the choices you've made: {[yes, no, yes, yes, no, ..., yes], [yes]}. Going back one level would then be about traversing the queue and going down the tree following each decision except the last one in the zipper list. If you want to go up 4 levels, you need to go back 4 elements in the zlist, then down the tree. Again, this is not exactly optimal. By transforming a binary tree into a zipper, it becomes simpler to handle everything.
This is done by storing the past part of the tree (the previous node and the paths you didn't take) every time you go down a level. When going back up, just graft the child back onto the parent. Here's the initial tree:

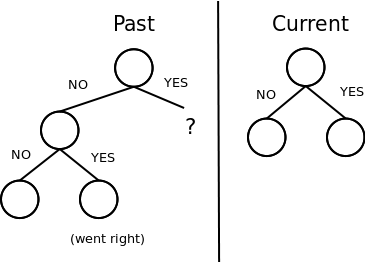
And here's what the zipper could look like once choosing 'yes' once:
And then picking 'no':
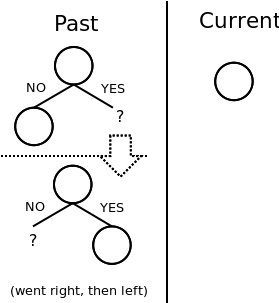
As described above, when going back up a level, take the part on the 'current' side, and put it as the right child (because we went to the right) of the past tree. That will give you the original tree back.
To represent this in Erlang, we'll need a few constructs. First of all, a node of a tree (which would hold the questions and then the left and right branch) can be defined either as the atom undefined or as a tuple of the form {fork, Question, Left, Right}, where Left and Right are both nodes themselves.
The 'past' section will be called a thread and will be a stack of previously seen branches (or choices in the code below). A branch is simply a tuple containing the direction that was taken and the tree without the 'current' section. This will give a zipper of the form {Thread = [{Direction, Value, ParentNode}|_], CurrentNode}.
Here it is as implemented in the zbintrees module:
-module(zbintrees).
-export([root/1, get/1, put/2, right/1, left/1, top/1,
set_left_branch/2, set_right_branch/2]).
-compile({no_auto_import,[get/1, put/2]}).
-type node(A) :: undefined
| {fork, A, Left::node(A), Right::node(A)}.
-type choice(A) :: {left, A, node(A)}
| {right, A, node(A)}.
-type thread(A) :: [choice(A)].
-type zipper(A) :: {thread(A), node(A)}.
%% Creates a basic binary zipper tree. Should be called first when
%% declaring the data structure
-spec root(A) -> zipper(A).
root(A) -> {[], {fork, A, undefined, undefined}}.
%% Fetches the value of the current position
-spec get(zipper(Val)) -> Val.
get({_Thread, {fork, Val, _Left, _Right}}) -> Val.
%% Either replaces or create a new node (if it was 'undefined')
%% at the current position in the zipper binary tree. The
%% value of the node is the one in the second argument.
-spec put(A, zipper(A)) -> zipper(A).
put(Val, {Thread, undefined}) ->
{Thread, {fork, Val, undefined, undefined}};
put(Val, {Thread, {fork, _OldVal, L, R}}) ->
{Thread, {fork, Val, L, R}}.
%% Moves down the tree one level, picking the right child.
-spec right(zipper(A)) -> zipper(A).
right({Thread, {fork, Val, L, R}}) -> {[{right, Val, L}|Thread], R}.
%% Moves down the tree one level, picking the left child.
-spec left(zipper(A)) -> zipper(A).
left({Thread, {fork, Val, L, R}}) -> {[{left, Val, R}|Thread], L}.
%% Moves back up one level. When doing so, it reassembles the
%% Current and Past parts of the trees as a complete node.
-spec top(zipper(A)) -> zipper(A).
top({[{left, Val, R}|Thread], L}) -> {Thread, {fork, Val, L, R}};
top({[{right, Val, L}|Thread], R}) -> {Thread, {fork, Val, L, R}}.
%% Shortcut function to add a left child
set_left_branch(A, Zipper) ->
top(put(A, left(Zipper))).
%% Shortcut function to add a right child
set_right_branch(A, Zipper) ->
top(put(A, right(Zipper))).
And you can also get the unit tests. An example usage of the tree could look a bit like what follows:
1> Tree = {[], {fork,
1> "Open door?",
1> {fork,
1> "Enter hallway?",
1> {fork, "you die alone.", undefined, undefined},
1> {fork, "you die in a hallway", undefined, undefined}},
1> {fork,
1> "Eat the bacon?",
1> {fork, "You die of hunger", undefined, undefined},
1> {fork,
1> "Eat more bacon?",
1> {fork, "You die of hunger", undefined, undefined},
1> {fork, "Hooray for bacon!", undefined, undefined}}}}}.
{[],
{fork,"Open door?",
{fork,"Enter hallway?",
{fork,"you die alone.",undefined,undefined},
{fork,"you die in a hallway",undefined,undefined}},
{fork,"Eat the bacon?",
{fork,"You die of hunger",undefined,undefined},
{fork,"Eat more bacon?",
{fork,"You die of hunger",undefined,undefined},
{fork,"Hooray for bacon!",undefined,undefined}}}}}
2> zbintrees:get(Tree).
"Open door?"
3> zbintrees:get(zbintrees:right(Tree)).
"Eat the bacon?"
4> zbintrees:get(zbintrees:left(zbintrees:right(Tree))).
"You die of hunger"
5> zbintrees:get(zbintrees:top(zbintrees:left(zbintrees:right(Tree)))).
"Eat the bacon?"
6> zbintrees:get(zbintrees:right(zbintrees:top(zbintrees:left(zbintrees:right(Tree))))).
"Eat more bacon?"
7> zbintrees:get(zbintrees:right(zbintrees:right(zbintrees:top(zbintrees:left(zbintrees:right(Tree)))))).
"Hooray for bacon!"
8> "I won!".
"I won!"
I cheated the tree creation by doing it with the internal representation, but yeah. As the 'game' goes, you can see that I actually die ("You die of hunger"), then use the zbintrees:top/1 function to go back a level and keep going. A real world use would likely go through these steps in an imperative manner rather than just chaining the functions the way I do.
Zipper Forests
The zipper binary trees were fine for the simplified 'yes/no' decision tree, but the use cases are kind of limited. How many things can you think of where a binary tree going both up and down is really necessary? It's a bit more useful to have trees with as many nodes as you want. To build one, I'll use a structure similar to that is used in N-ary trees. N-ary trees usually have a maximum number of elements on each level, but for the purpose of simplicity I won't limit the number of elements.
A simple way to do things with N-ary trees is to hold each nodes of a level in a list. As such, one of our n-trees could look a bit like:
[a, b, c, d]
/ | | \
[l,m,n] [o] [p,q,r] [s,t,u,v,x]
|
[1,2,3,4,5,6,7,8,9]
How to make this into a zipper? It's not just storing left or right and then rejoining the nodes like with zipper binary trees. Fortunately, we had zipper lists. By using them, we can simulate going from left to right and have an 'unlimited' number of nodes on each level. By nesting lists, we get the n-ary tree behavior we need.
The structure of the tree will go as follows. Each node has the form {Value, Children}. These nodes go into a zipper list to form a znode (I'm just coining terms/types for the hell of it). Each level of the tree is a znode. The tree as a whole has the form {Thread, Znode}. The following tree would be a valid zipper n-tree:
{[], % thread
{[], [{a, {[], [{d, {[], []}},
{e, {[], []}}]}},
{b, {[], [{f, {[], []}},
{g, {[], [{k, {[], []}}]}}]}},
{c, {[], [{h, {[], []}},
{i, {[], []}},
{j, {[], []}}]}}]}}.
Or in a more visual manner:
[a, b, c]
/ | \
[d,e] [f,g] [h,i,j]
\
[k]
I should already say that it's a bit of a misnomer to call them 'zipper n-trees' given I don't enforce the limit, but I'll stick to it for this post. I'll go as far as naming the module zntrees. The module supports basic operations: inserting, replacing, deleting values, creating an empty tree, moving to the left and right, and going to the current element's children or parent:
-module(zntrees).
-export([root/1, value/1,
replace/2, insert/2, delete/1,
left/1, right/1, children/1, parent/1, rparent/1]).
-type zlist(A) :: {Left::list(A), Right::list(A)}.
-type znode() :: zlist({term(), zlist(_)}). % znode is a zlist of nodes
-type thread() :: [znode()].
-type zntree() :: {thread(), znode()}.
%% creates a tree with an empty thread and Val as the root.
-spec root(term()) -> zntree().
root(Val) -> {[], {[], [{Val, {[], []}}]}}.
%% Extracts the node's value from the current tree position.
-spec value(zntree()) -> term().
value({_Thread, {_Left, [{Val, _Children} | _Right]}}) -> Val.
%% Replaces the value from at the current tree position, without touching
%% the children nodes.
-spec replace(term(), zntree()) -> zntree().
replace(Val, {T, {L, [{_Val, Children}|R]}}) ->
{T, {L, [{Val,Children}|R]}}.
%% Add a new node at the current position with the value Val.
-spec insert(term(), zntree()) -> zntree().
insert(Val, {Thread, {L, R}}) ->
{Thread, {L, [{Val, {[], []}} | R]}}.
%% Deletes the node at the current position and its children.
%% The next one on the right becomes the current position.
-spec delete(zntree()) -> zntree().
delete({Thread, {L, [_|R]}}) ->
{Thread, {L, R}}.
%% Moves to the left of the current level.
-spec left(zntree()) -> zntree().
left({Thread, {[H|T], R}}) ->
{Thread, {T, [H|R]}}.
%% Moves to the right of the current level
-spec right(zntree()) -> zntree().
right({Thread, {L, [H|T]}}) ->
{Thread, {[H|L], T}}.
%% Goes down one level to the children of the current node.
%% Note that in order for this to work, the {Val, Children} tuple
%% needs to be broken in two: the value goes in the Thread's zlist
%% while the Children become the current level.
-spec children(zntree()) -> zntree().
children({Thread, {L, [{Val, Children}|R]}}) ->
{[{L,[Val|R]}|Thread], Children}.
%% Moves up to the direct parent level. Doesn't rewind the current
%% level's zlist. This means that if you have a tree, go to the
%% children, browse to the right 2-3 times, then go back up and
%% down to the children again, you'll be at the same position you were
%% before.
%% If you prefer the children to be 'rewinded', use rparent/1.
-spec parent(zntree()) -> zntree().
parent({[{L, [Val|R]}|Thread], Children}) ->
{Thread, {L, [{Val, Children}|R]}}.
%% Moves up to the direct parent level, much like parent/1. However,
%% it rewinds the current level's zlist before doing so. This allows
%% the programmer to access children as if it were the first time,
%% all the time.
-spec rparent(zntree()) -> zntree().
rparent({[{ParentL, [Val|ParentR]}|Thread], {L, R}}) ->
{Thread, {ParentL, [{Val, {[], lists:reverse(L)++R}}|ParentR]}}.
And now you can declare trees with any number of nodes. See the unit tests if you want.
The use cases for such trees are more abundant: undo trees, XML navigating with DOM, representing more complex 'choose your own adventure' books (or decision trees), directories in a filesystem, etc.
Here we'll try a DOM tree example with the following fake document:
<html>
<header>
<title>Hello, World!</title>
</header>
<body>
<h1>Hello, World!</h1>
<p>How are you, planet?</p>
<ul>
<li>Bat</li>
<li>Man</li>
<li>Na Na Na Na</li>
</ul>
</body>
</html>
You could build the tree as a zntree by using the functions root/1, children/1, insert/2, right/1 and parent/1, but this would be a little too verbose, so I'll declare it in it's final form:
1> Document =
1> {[],
1> {[],
1> [{html,
1> {[],
1> [{header,
1> {[],
1> [{title, {[],[{"Hello, World!",{[],[]}}]}}]}},
1> {body,
1> {[],
1> [{h1,{[], [{"Hello, World!", {[],[]}}]}},
1> {p, {[], [{"How are you, planet?", {[],[]}}]}},
1> {ul,
1> {[],
1> [{li, {[],[{"Bat", {[],[]}}]}},
1> {li, {[],[{"Man", {[],[]}}]}},
1> {li, {[],[{"Na Na Na Na", {[],[]}}]}}]}}]}}]}}]}}.
{[],
{[],
[{html,{[],
[{header,{[],[{title,{[],[{"Hello, World!",{[],[]}}]}}]}},
{body,{[],
[{h1,{[],[{"Hello, World!",{[],[]}}]}},
{p,{[],[{"How are you, planet?",{[],[]}}]}},
{ul,{[],
[{li,{[],[{[...],...}]}},
{li,{[],[{...}]}},
{li,{[],[...]}}]}}]}}]}}]}}
Ugly, but yeah. We can now play and navigate around the tree. The functions left/1 and right/1 can be used to access the current element's siblings while parent/1 and children/1 can be used to go up and down the hierarchy:
2> zntrees:value(zntrees:children(Document)).
header
3> zntrees:value(zntrees:right(zntrees:children(Document))).
body
4> Body = zntrees:right(zntrees:children(Document)).
<huge structure>
5> zntrees:value(zntrees:right(zntrees:right(zntrees:children(Body)))).
ul
6> List = zntrees:right(zntrees:right(zntrees:children(Body))).
<huge structure>
7> zntrees:value(zntrees:children(zntrees:left(zntrees:rparent(zntrees:right(zntrees:children(List)))))).
"How are you, planet?"
That last one is a bit exaggerated, I agree. Anyway, this zipper makes it possible to change a node's value in constant time. In the following example, I'll go to the first element of the list and replace "Bat" by "Platypus". The log n modifications needed to rewrite the data structure in normal trees are now amortized over the calls to parent/1, if you ever actually need to call it (if you don't, you never really have to pay that rewrite cost):
8> NewDocument = zntrees:replace("Platypus", zntrees:children(zntrees:children(List))).
<huge structure>
9> zntrees:parent(zntrees:parent(zntrees:parent(zntrees:parent(NewDocument)))).
{[],
{[],
[{html,{[{header,{[],
[{title,{[],[{"Hello, World!",{[],[]}}]}}]}}],
[{body,{[{p,{[],[{"How are you, planet?",{[],[]}}]}},
{h1,{[],[{"Hello, World!",{[],[]}}]}}],
[{ul,{[],
[{li,{[],[{"Platypus",{[],[]}}]}},
{li,{[],[{"Man",{[],...}}]}},
{li,{[],[{"Na Na Na Na",{...}}]}}]}}]}}]}}]}}
DOM navigation is only one of the possible uses of zipper trees. As I mentioned earlier, undo trees or decision trees are also possible. In fact, this kind of zipper can be used to represent any undirected acyclic graph or forest: this means (I believe) that many graph-based problems where no cycle exist can be represented and navigated with the above zipper, including concepts such as minimum spanning trees. This could be useful, if anyone ever needed to do that kind of stuff in Erlang I guess. Which brings me to my next point...
Alternatives to Zippers
Zippers can be pretty useful when you need a specific way to quickly update a datastructure as shown above. Depending on the use case, using adjacency lists (or something close to that) with dicts, gb_trees or ETS tables can prove to be practical: those would in fact allow shared access and modifications to the data structures, something that sounds conceptually harder to do with zippers.
Anyway, I hope this was an educative/entertaining/distracting or anything not negative read.