“My bad opinions”

Simhashing (hopefully) made simple

Why Simhash?

When it comes to figuring out how similar various pieces of data are from one another (and which is the closest matching one in a large group of candidates), simhashing is one of my favourite algorithms. It's somewhat simple, brilliant in its approach, but still not obvious enough for most people (myself included) to come up with it on their own. Readers may be familiar with hashing algorithms such as MD5 or SHA, which aim to very quickly create a unique signature (hash) of the data. These functions are built so that identical files or blobs of data share the same hash, so you can rapidly see whether two blobs are identical or not, or if a blob still has the same signature after transmission to see if it was corrupted or not. Then different blobs, even if mostly the same, get an entirely different signature.

While simhashes still aim to have unique signatures for documents, they also attempt to make sure that documents that look the same get very similar hashes. That way, you can look for similar hashes to figure out if the documents are closely related, without needing to compare them bit by bit. It's a statistical tool to help us find near-duplicates faster.

That's a bit vague, but that's alright. I'll try to explain things in a way that gives a good understanding of things.

Reinventing Simhashes

Let's first take a look at ASCII. The character 'a', in ASCII, is the number 97, or in a binary representation, 01100001. All letters of the basic English alphabet can be represented that way:

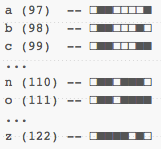
This is nothing new to most programmers out there. I could also represent entire words with sequences of these binary values:

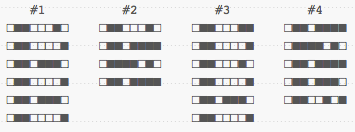
Some readers will be able to read binary and ASCII straight away and know what these words are. We can easily see that the first 3 most significant bits (on the left) of all letters are the same, and we could discard them, getting:

If I were to ask you to group these words in two pairs of most similar to each other, chances are that you would put #1 and #3 together, and #2 and #4 together. You would be right to do so. The four words, in order, are "banana", "bozo", "cabana", and "ozone".

By looking at the binary patterns, our brains are able to figure out a few things naturally. The position of each bit, the length of the word, the repetition of sequences of bits, and how 'light' or 'dark' a column looks are a few things we may pick up as some kind of signature of each word.

What's interesting is that each of these signatures is unique, yet we're somehow able to figure out how similar they are based on that. Compare this to the following four MD5 hashes of the same strings:

    72b302bf297a228a75730123efef7c41
    e1c8d6347c0c24e5cbc60e508f3fc1b5
    da5e04f2b94deec3c70632f77644a041
    1b9ac7aecd52eab14089942f8267f22a

There's no way to know at a glance which is closer to the other. Again, there's nothing surprising there, given MD5 is not meant for hashes to be similar.

While our visual layout was nice to figure out how to match short words together, it's utterly impractical to use such visual signatures in a general manner -- programming software to recognize them the way a human would would take forever, and it would be slower than just comparing letters one by one.

What we have, though, is the idea that using the binary representation of a blob of data may be enough to create a decent signature that does respect similarity -- a simhash.

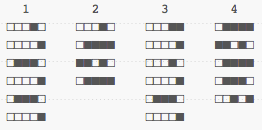
What could be nice would be to be able to compress the information a bit, so it's a bit more obvious what it contains. We could build a histogram of all the binary values: add 1 for each bit set to 1 in a column, the rest is skipped. This could give us an interesting layout, a bit like follows (I'm making bars horizontal):

That's not very good. The problem is that we're only looking at half the data. We're discarding all the 0 bits. Let's try doing it by pretending each empty bit (white square) is worth -1, and that others (black squares) are worth +1. We could represent things like sums:

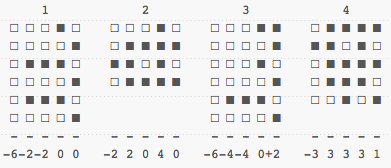
Let's try it a bit more visually, representing each sum as a little histogram, again:

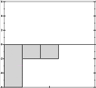
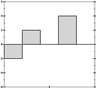
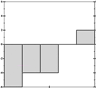
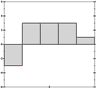
It's now easier to see which is closest to which, if you squint right. It may even be easier to do so than when we had the full patterns in view, and we're doing it with a fraction of the data we had before. We're getting a decent signature.

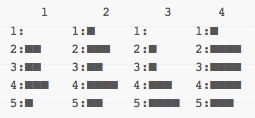
Let's push it a bit further. I'll take each of these final histograms, and for each value above or equal to 0, I'll fill a bit. For each value under 0, I'll leave it empty. My four signatures are now:

Hot damn, that worked fine. In this case, we instantly see which are to be paired together. 1 and 3 obviously fit together, given they're the same, and 2 and 4 go together, as they get the same signature.

How would we find the distance between signatures when none of them are identical? If we had a piece of data resulting in the hash 10011, which one would it be the closest to? It turns out that using the Hamming Distance is a decent way of doing it. The Hamming Distance is, in a nutshell, a way to look at two sequences of numbers, letters, or whatever piece of data, and see how different they are.

With a bunch of groups of bits of the same length, it's done by looking at them one by one. Every time they're different, we add 1 to the hamming distance. If they're the same, we leave it as is. As such, the Hamming Distance between our two previous signatures and our new pattern is:

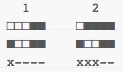
Our new pattern has a hamming distance of 1 compared to signatures 1 and 3, and a distance of 3 compared to signatures 2 and 4. As such, we can say that the new signature is likely to be more similar to 1 than 2.

Now it's well possible that things are very similar according to our current simhashing without looking that way to the human eye -- the string "sssss" would have given us a signature closer to "banana" than "bozo", for example, with a distance of 1. There are good explanations for that.

What Did we Just Do?

We just implemented a very, very basic version of the simhash algorithm. Why what we did works requires a bit of math. This is where the simhash papers tend to flex their statistical muscles. To make it short and overly simple, when we take fragments of an entire binary blob (here we took segments of 6 bits out of a stream of ones and zeroes), we're taking some kind of snapshot of the whole thing, and giving it weight based on how often it happens.

Let's look at our words again, but this time, by sorting letters by their most significant bits:

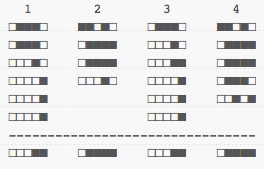
This makes it a bit easier to see how the frequency of each letter (or rather, each feature, as the papers call them) has an impact on the final value. If we have many identical letters (features), no matter their order, then the chances are signatures look rather similar in the end when we 'collapse' the whole thing into a tiny 5-bit hash.

This raises a few questions:

1. If the order of features is not important, how do we make it understand that strings like "hahahahaha!" have a somewhat different meaning from "aaaaaaahhhhhhh!"?
2. What do we do when letters that are way different have a rather similar binary representation? It would kind of suck that "cc" is seen as similar to "bababababa", as they should give a very similar signature under our current scheme.
3. How can we deal with data that is not ASCII text, where features may be of varying sizes?

In fact, these three questions are somewhat related to figuring out a way to make significant hashes be longer than 5 or 8 bits, and giving it a regular length.

Improving the Distribution of Bits

The first easy way to improve the distribution of the bits in our feature is to pass them through some kind of function that keeps unique values, but makes them vary a lot even when they're similar. Does this ring a bell?

Hashing algorithms like MD5, SHA, or even your common hashmap's hashing function will do this just fine. In fact, passing a letter through a MD5 hashing algorithm will give me 128 bits of data that is not too likely to be similar to the one obtained from other values. What's nice is that it will also let me take larger features (say a Unicode sequence of code points that requires multiple bytes to be represented) and give it the same weight as an ASCII character.

By passing each feature (no matter what its size is) through a normal hashing function, we allow to give them all an identical weight. We can then calculate our simhash the same way we did earlier, but with the binary values from the new intermediary hash function.

This is interesting because if I do that, instead of using letters, I may as well use words for my simhash. Maybe the word "cat" will give me 01011001010111, and that "romanesque" will give me 01000101001101. It will then be possible to build simhashes out of much larger vocabularies by choosing what we consider to be a feature, and what isn't.

We could solve the "aaaaaaahhhhh!" versus "hahahahaha!" problem by making syllables a feature: "ah" and "aa" and "hh" and "!" could be seen as different features. We would then be guaranteed a different result than if we took everything letter by letter.

The second aspect of it is being able to give a weight to each feature. Let's imagine for a moment that we have 3 files on disk:

1. hello.txt: "hello world"
2. hello.pdf: "hello world" (in PDF)
3. hackers.pdf: "they're trashing our rights!" (in PDF also)

We want to simhash them according to their content, not their binary representation on disk. If we use simhashing over the whole file, we'll find out that the two PDF files are seen as very similar. That's because PDF is a heavier format than a .txt file, with metadata, headers, and some common structure that will overweight the content in many cases.

Another example is finding which of the following 3 sentences are the closest together:

1. "the cat in the tree is white"
2. "the man in the suit is happy"
3. "a white cat is in a tree"

For a human reading this, it might be preferable to have sentences 1 and 3 closer together as they clearly talk about white cats in trees, whereas the sentence 2 is about something else entirely. Here are all the (fictional) hashes for the words in these sentences:

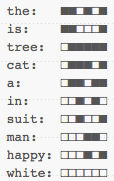
The three sentences can then have the following signatures (which I pre-sorted to make them easier to deal with):

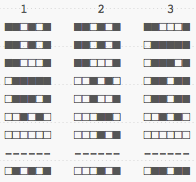
And the distance between each:

Based on this one, sentences 1 and 2 are very close. How can we bring it the meaning we want? The solution is to create weighed features. To do this, I could take words used frequently, with little meaning in the sentence like 'a', 'the', and 'in' and give them a weight of 1, and take more unusual words like 'man', 'happy', or 'cat' and give them a weight of 3.

When counting values, instead of doing +1 or -1, I do +Weight or -Weight, effectively giving me the following signatures:

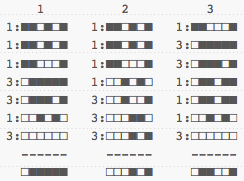
Re-calculating the distances, we get:

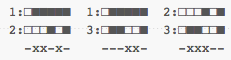
And as we hoped, strings 1 and 3 are now the closest with a Hamming distance of two.

Anything Else?

No, not really. As far as simhashing is concerned, that's it! The complexity now lies in figuring out ways to build 'vocabularies' (dictionaries of weighted features) that are relevant to what we're trying to match: if you're interested in the structure of XML documents but not their text, serializing tree hierarchies and node types as features may be an approach that makes more sense to you than for someone who's looking to know if the textual content of an HTML site changed or not even when the structure itself changed.

Building good vocabularies is where a huge part of the challenge lies when it comes to making simhashes useful. The other tricky area is figuring out how to be able to quickly match simhashes together. Comparing a ton of simhashes together to find the best matches still is a complex problem the same way it would be without simhashes: what you gain, however, is how much space it takes to store all the items to compare, and how long each comparison will be. For big files, it's quite an improvement already, but it won't compensate for large values of N if you have an O(n²) algorithm to compare everything. There are a few papers freely available on the question if you're interested.

I hope I managed to make simhashing understandable and interesting as an algorithm. There are all kinds of interesting applications where simhashes could shine, from trying to figure out how similar data structures are, finding out if the layout or the content of a website you scrape changed, detecting spam[PDF] or real-time merging of near-duplicate log events.